命令式语言中一般实现 Queue 就是用一个链表或数组做存储，之后有两个引用 Head 和 Tail 分别指向队首和队尾。一般为了方便判断队列是否为空还会引入一个哑元，Head 引用不直接指向队列内的第一个元素而是指向这个哑元。具体细节可以参看各种数据结构相关的介绍。

不过在函数式语言下，各种数据结构都是不可变的，不会有个 Head、Tail 引用去指向队首队尾，并在每次有元素入队出队的时候被更新。在这种情况下该怎么实现 Queue 呢？

两个 Stack 来实现 Queue

以前遇到过这么一个面试题：怎么用两个 stack 去实现一个 queue？当时在做这个题的时候并没有想太多，只是把它当做一个思考题来做，但这个问题实际是对怎么在函数式语言下实现不可变队列有帮助的。

不可变队列实现的难点就是因为没有 Head、Tail 引用，用单个链表或数组在不考虑扩容的情况下，都是只能在队列的一端以 O(1) 的时间增加一个元素，但要从队列另一端取元素需要遍历整个队列导致时间复杂度变为 O(n)。这个时间复杂度并不符合我们的期待。而使用两个用链表实现的 Stack 去实现队列就能做到出入队平均时间复杂度都为 O(1)。注意是平均时间复杂度。

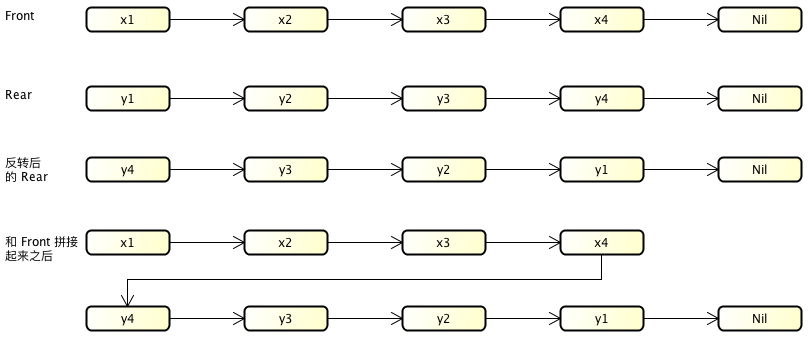
如上图所示，用两个链表分别称为 Front 和 Rear。每次入队时，都将新元素添加到 Rear 链表中，这样时间为 O(1)。每次出队时，都从 Front 队列中取元素出队。如果 Front 非空，那么出队的时间复杂度为 O(1)，如果 Front 为空，则将 Rear 链表反转一下作为新的 Front 队列。之后再将新 Front 队列的队首元素出队，这个过程的时间复杂度为 O(n)。假设 Front 为空时 Rear 链表元素数量为 m，那么将 Rear 反转的时间是 O(m) 但之后 m 个元素出队时时间都是 O(1)，于是能将反转 Rear 队列的时间平摊给之后 m 次出队时间，所以平均下来出队操作的时间还是 O(1)。

这个过程用 Clojure 实现如下：

(defrecord Queue [front rear cnt])
(defn make-queue
  ([] (Queue. '() '() 0))
  ([front rear cnt]
    (Queue. front rear cnt)))
(defn- maintain [queue]
  (if (and (empty? (.-front queue)) (not-empty (.-rear queue)))
    (make-queue (reverse (.-rear queue)) '() (.-cnt queue))
    queue))
;; maintain after every enqueue to insure front list 
;; must have at least one element when queue is not empty
(defn enqueue [queue x]
  (maintain (make-queue (.-front queue) (conj (.-rear queue) x) (inc (.-cnt queue)))))
(defn empty-queue? [queue]
  (zero? (.-cnt queue)))
(defn peek [queue]
  (when-not (empty-queue? queue)
    (first (.-front queue))))
(defn dequeue [queue]
  (if-not (empty-queue? queue)
    (maintain (make-queue (rest (.-front queue)) (.-rear queue) (dec (.-cnt queue))))
    queue))

maintain 函数的作用主要是为了让队列非空时，Front 链表至少有一个元素存在。不然队列的 peek 操作在 Front 为空时需要遍历 Rear 链表才能找到下一个出队元素，并且由于 peek 的返回值只有下一个出队的元素，我们不能将新的队列结构返回(即反转 Rear 链表并将其作为 Front)，于是在连续执行 peek 操作时，每次 peek 都要遍历整个 Rear 表。这个是不合理的，所以我们需要保证队列非空时，Front 链表至少有一个元素存在，以供 peek 使用。

Lazy 来实现真正 O(1) 的队列

上面实现的缺陷是显而易见的，虽然平均时间是 O(1) 但毕竟会存在某次出队的耗时为 O(n)，导致使用时每次出队操作时间有颠簸。而如果我们能借助函数式编程语言普遍支持的 Lazy 特性去实现队列，就能避免这种颠簸。

还是延续上面双链表的实现，最耗时的操作是反转 Rear 链表，每次执行这个操作的时间点是在 Front 队列为空的时候。如果我们不想只在这一个时间点进行 Rear 反转，想将反转过程平摊到每次出入队操作中，那么我们就需要在 Front 还未变为空的时候就执行 Rear 反转，并且每次都执行一小步，比如反转一个元素，从而保证每一个出入队操作的时间都是 O(1)。

但是 Front 链表非空时我们就反转 Rear 的话，反转完 Rear 时如果队列没有元素出队，那么 Front 链表是没有变动过的，那不可能像之前一样将反转后的 Rear 链表直接作为 Front 来使用，而是还需要将 Front 和反转后的 Rear 连接起来。Front 是链表，头部是队首，如下图所示，如果直接拼接的话还是要遍历 Front 链表找到 Front 链表的尾巴，再将尾巴指向反转后的 Rear 链表。

如果 Rear 长度是 n，Front 长度是 m，那么反转 Rear 的操作要 n 步，连接 Front 的操作要 m 步。以连续入队操作来看，也就是说如果每次入队都执行一个 Rear 反转或者连接 Front 工作的话，连接完毕后 Rear 又会有 m + n 个元素了，我们为了每次入队都只执行一次额外操作，所以每一个入队操作都不能浪费，也就是说连接完毕之后再入队一个元素时我们又要开始下一轮反转 Rear 和连接 Front 的工作，此时 Front 长度为 m + n，Rear 长度为 m + n + 1，从而得到 Rear 反转和连接 Front 的工作每次是 Rear 比 Front 多一个元素的时候开始。

我们将反转 Rear 和连接 Front 两个工作称为 rotate，并且约定 rotate 执行时间为 Rear 比 Front 多一个元素时。我们得到 rotate 函数如下，注意 acc 表示的是反转 Rear 的结果，即 rotate 的反转 Rear 和连接 Front 操作最终都是构建在 acc 这个 List 上。

// rotate 执行时必须保证 rear 比 front 多一个元素
(defn rotate [front rear acc]
  (lazy-seq
    (if (empty? front)
      // 如果 front 为空，那么 rear 只有一个元素，所以直接放入 acc
      (cons (first rear) acc)
      // 当 front 非空，下面解释
      (cons (first front)
            (rotate (rest front) (rest rear) (cons (first rear) acc))))))

front 非空的情形直接这么看比较难理解，不过通过下面公式就好理解了：
rotate(X, Y, A) = X ++ reverse(Y) ++ A
= x1 ++ (X’ ++ reverse(Y) ++ A)
= x1 ++ X’ ++ reverse(Y’) ++ y1 ++ A
= x1 ++ rotate(X’, Y’, y1 ++ A)

其中 x1 是 X 中的第一个元素，y1 是 Y 中的第一个元素。A 是用来存放 Rear 反转结果的。

rotate 的结果实际就是 Front，我们希望出队入队都能执行 Rear 反转或连接 Front，所以我们每次入队出队都要求 rotate 结果下一个值。所以单独拿一个叫做 rots 的 var 来存放 rotate 的结果，rots 和 front 共同指向 rotate 的结果，只是 rots 是用来每次出队入队时候求值的，front 仅仅在出队时使用，相当于 front 保存着队首元素，rots 只是为了求出整个队列，所以不需要保存队首元素。

使用 Clojure 实现如下：

(defrecord LazyQueue [front rear rots cnt])
(defn make-queue
  ([] (LazyQueue. '() '() '() 0))
  ([front rear rots cnt] (LazyQueue. front rear rots cnt)))
(defn rotate [front rear acc]
  (lazy-seq (if (empty? front)
              (cons (first rear) acc)
              (cons (first front)
                    (rotate (rest front) (rest rear) (cons (first rear) acc))))))
(defn maintain [queue]
  (if (empty? (.-rots queue))
    (let [rots (rotate (.-front queue) (.-rear queue) '())]
      (make-queue rots '() rots (.-cnt queue)))
    (make-queue (.-front queue) (.-rear queue) (rest (.-rots queue)) (.-cnt queue))))
(defn enqueue [queue x]
  (maintain (make-queue (.-front queue) (conj (.-rear queue) x) (.-rots queue) (inc (.-cnt queue)))))
(defn empty-queue? [queue]
  (zero? (.-cnt queue)))
(defn peek-queue [queue]
  (when-not (empty-queue? queue)
    (first (.-front queue))))
(defn dequeue [queue]
  (maintain (make-queue (rest (.-front queue)) (.-rear queue) (.-rots queue) (dec (.-cnt queue)))))

那么 Clojure 中的 Queue 是怎么实现的呢？

Clojure 中的 queue

Clojure 中的 queue 一般是指 clojure.lang 中的 PersistentQueue，它使用起来可能会让人觉得有点怪，比如像这样：

(let [queue (-> (PersistentQueue/EMPTY)
                (conj 1)
                (conj 2)
                (conj 3))]
  (loop [q queue]
    (when-let [x (peek q)]
      (println x)
      (recur (pop q)))))

它出队用的 peek 和 pop，让人感觉像个 stack 一样。用 first 和 rest 在一些场合下也行，first 使用起来跟 peek 效果相同，但 rest 会将队列转换为 list，从而失去 queue 的语义，转换成 list 之后再使用 conj 会将新元素加入到 list 首部。

PersistentQueue 实现方式跟前面说的两个 Stack 实现 Queue 有点类似，但里面 Front 是 List，Rear 是 PersistentVector。入队函数实现如下：

public PersistentQueue cons(Object o){
    if(f == null)     //empty
        return new PersistentQueue(meta(), cnt + 1, RT.list(o), null);
    else
        return new PersistentQueue(meta(), cnt + 1, f, (r != null ? r : PersistentVector.EMPTY).cons(o));
}

看到入队的时候也是直接放入 Rear，并且也是只要 Queue 不空则至少有一个元素再 Front 中。

出队函数如下：

public PersistentQueue pop(){
    if(f == null)  //hmmm... pop of empty queue -> empty queue?
        return this;
    ISeq f1 = f.next();
    PersistentVector r1 = r;
    if(f1 == null)
        {
        f1 = RT.seq(r);
        r1 = null;
        }
    return new PersistentQueue(meta(), cnt - 1, f1, r1);
}

出队时从 Front 出队，如果出队完 Front 为空，则需要将 Rear 导入 Front。由于 Rear 是由 PersistentVector 实现的，每次添加元素是以接近 O(1) 的时间添加在 vector 末尾，所以其元素顺序和 Front 顺序相同，可以直接将 Rear 通过 seq 操作转化为 List 后作为 Front 即可，无需进行反转操作。因为 PersistentVector 能够以 O(1) 的时间访问任意一个元素，所以它只需要实现 ISeq 接口就能变成一个 List，不需要任何拷贝操作。

不需要反转，也不需要连接 Front (因为每次 Rear 变成 Front 时 Front 都是空的)，所以 PersistentQueue 不会出现“颠簸”，出队和入队基本都是 O(1) 的时间。

如此神奇的 PersistentVector 的实现可以看下这篇文章。

不可变队列的实现

不可变队列的实现

两个 Stack 来实现 Queue

Lazy 来实现真正 O(1) 的队列

Clojure 中的 queue